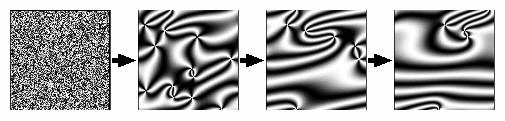
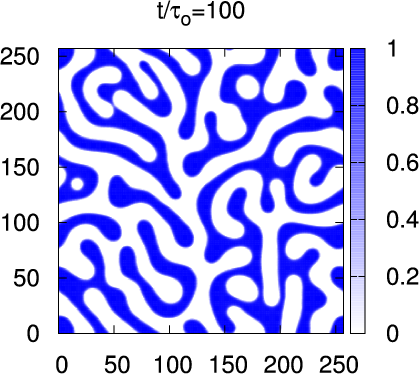
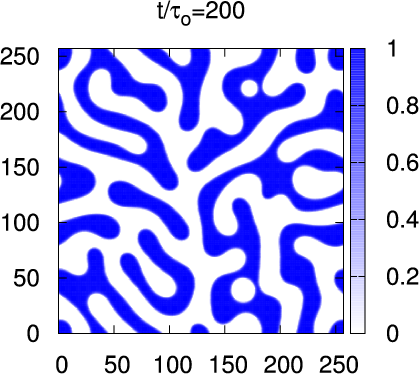
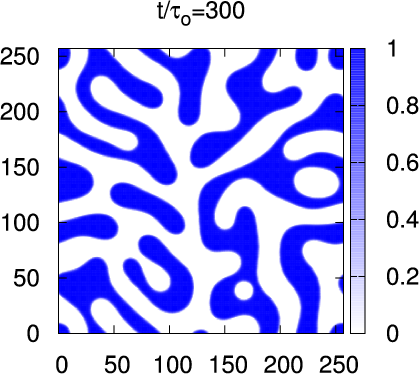
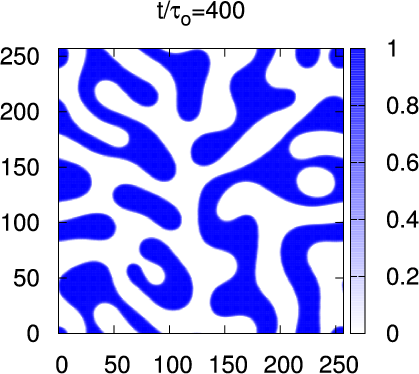
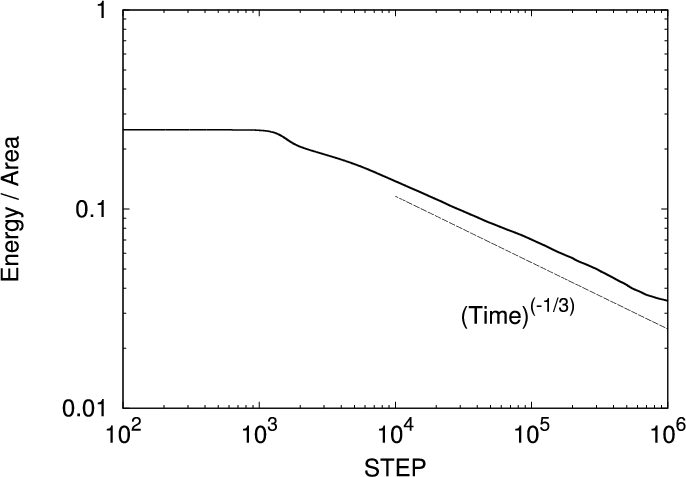
- Classification (Model A,B,C,D,H) comes from
P.C. Hohenberg and B.I. Halperin,
Review of Modern Physics 49, 435 (1977).
- modelA (Commnet)
- (MPEG)
- (MPEG)






- modelB (Commnet)
-
Dynamical Phase
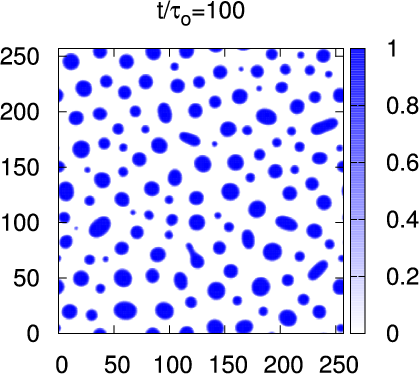
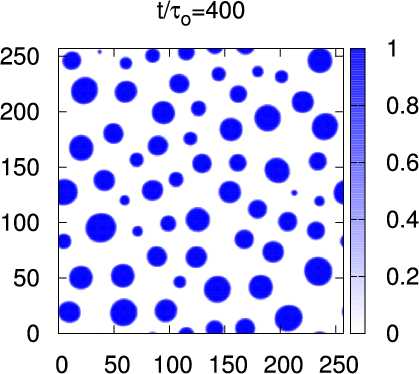
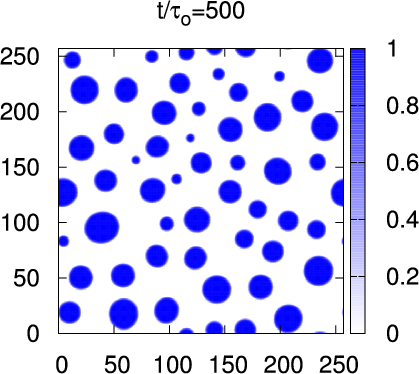
- Spinodal Decomposition
- Nucleation Growth
- phi=-0.70 (15:85)
(MPEG)

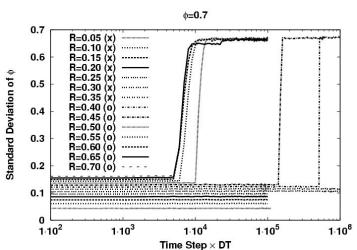
- phi=-0.70 (15:85)
(MPEG)
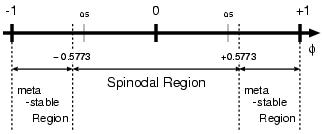
|phi_sp|=0.5773... (ca. 78.9:21.1) - modelC (MPEG) (Commnet)
- modelD (MPEG) (Commnet)
- modelH (MPEG) (Commnet)
- Isotropic System (Commnet)
- under shear flow

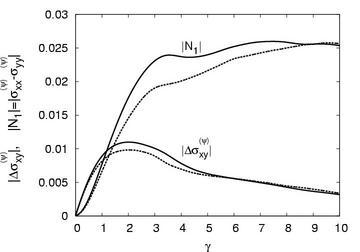
At around gamma=1~2, the shear stress shows a peak, where the domain
is elongated along (1,1,0)-direction. The 1st normal stress N_1
gradually increases with the imposed strain, gamma. Then, N_1 reaches
to a value at a steady state where the elongated domains are aligned
to (1,0,0)-direction.
(GIF)(Comment)
- Binary Alloy + Elastic Effect
- (a)Isotropic System
(MPEG)
(Commnet)
- (b)Anisotropic System(due to the Symmetry
of Crystal)(MPEG)(Commnet)
- (a)Isotropic System
(MPEG)
(Commnet)
- Viscoelastic Phase Separation (Polymer Solution) (Comment)
- Case 0 (Comment)
-
System0: Viscoelastic Phase Separation
(4.9Mbyte)(MPEG)
-
System1: Phase Separation of Binary Fluid Mixture
(from the same initial condition with System 0) (4.9Mbyte)(MPEG)
-
System0: Viscoelastic Phase Separation
(4.9Mbyte)(MPEG)
- Case 1 (Comment)
- Initial Configuration is same as Case 1,
but there is no viscoelastic effect. Simple Binary Fluid (model H)
(In order to compare with Case 0) - Parameter 1
(MPEG)(Comment)
- Parameter 2
(MPEG)(Comment)
- Parameter 3
(MPEG)(Comment)
- Case 0 (Comment)
- Block Copolymer
-
Phase Ordering Dynamics of Block Coplymer (1:1)
- Under No Shear Flow
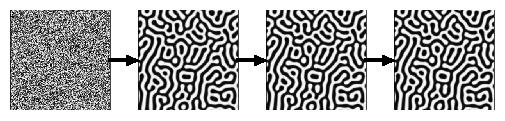
- Under Shear Flow (1:1)

- Under No Shear Flow
- Ordering Dynamics under no shear flow with Noise

- Ordering Dynamics under no shear flow
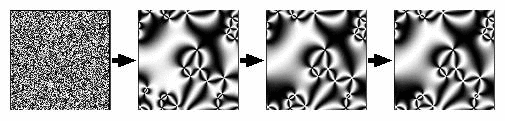
- Ordering Dynamics under shear shear flow